خصائص التحويل

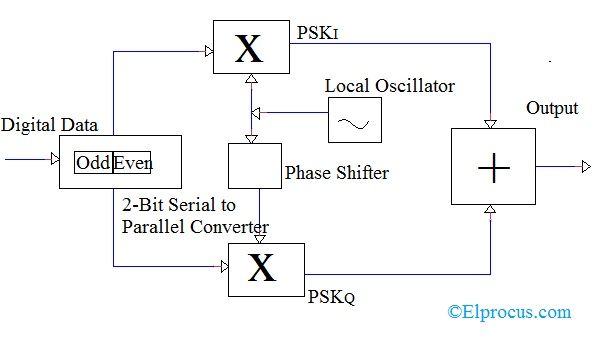
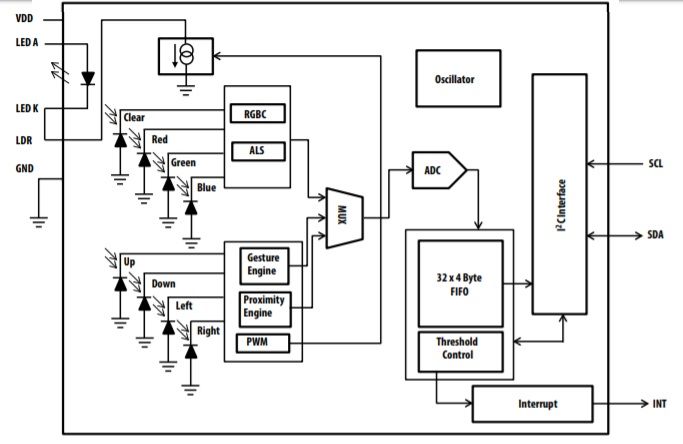
يمكن فهم خصائص النقل في الترانزستورات على أنها رسم لتيار خرج مقابل مقدار يتحكم في المدخلات ، مما يعرض بالتالي 'نقلًا' مباشرًا للمتغيرات من المدخلات إلى المخرجات في المنحنى الموضح في الرسم البياني.

نحن نعلم أنه بالنسبة لترانزستور الوصلات ثنائي القطب (BJT) ، يرتبط تيار جامع الإخراج IC وقاعدة إدخال التحكم IB بواسطة المعلمة بيتا ، والتي من المفترض أن تكون ثابتة للتحليل.

بالإشارة إلى المعادلة أدناه ، نجد علاقة خطية قائمة بين IC و IB. إذا جعلنا المستوى IB 2x ، فإن IC يتضاعف أيضًا بشكل متناسب.

ولكن للأسف ، قد لا يمكن تحقيق هذه العلاقة الخطية المريحة في JFETs عبر مقادير المدخلات والمخرجات. بدلاً من ذلك ، يتم تحديد العلاقة بين معرف تيار التصريف و جهد البوابة VGS بواسطة معادلة شوكلي :

هنا ، يصبح التعبير التربيعي مسؤولاً عن الاستجابة غير الخطية عبر المعرف و VGS ، مما يؤدي إلى منحنى ينمو بشكل أسي ، حيث ينخفض ​​حجم VGS.

على الرغم من أن اتباع نهج رياضي سيكون أسهل في التنفيذ لتحليل التيار المستمر ، إلا أن الطريقة الرسومية قد تتطلب تخطيط المعادلة أعلاه.

يمكن أن يعرض هذا الجهاز المعني وتخطيط معادلات الشبكة المتعلقة بالمتغيرات المماثلة.

نجد الحل بالنظر إلى نقطة تقاطع المنحنيين.

تذكر أنه عند استخدام الطريقة الرسومية ، تظل خصائص الجهاز غير متأثرة بالشبكة حيث يتم تنفيذ الجهاز.

نظرًا لتغير التقاطع بين المنحنيين ، فإنه يغير أيضًا معادلة الشبكة ، ولكن هذا ليس له أي تأثير على منحنى النقل المحدد بواسطة المعادلة أعلاه ، 5.3.

لذلك ، بشكل عام يمكننا أن نقول:

لا تتأثر خاصية النقل المحددة بواسطة معادلة Shockley بالشبكة حيث يتم تنفيذ الجهاز.

يمكننا الحصول على منحنى النقل باستخدام معادلة شوكلي ، أو من خصائص الإخراج كما هو مبين في الشكل 5.10

في الشكل أدناه ، يمكننا رؤية رسمين بيانيين. يقيس الخط العمودي مللي أمبير للرسمين البيانيين.

يرسم رسم بياني واحد معرف تيار التصريف مقابل VDS لجهد التصريف إلى المصدر ، والرسم البياني الثاني يرسم تيار التصريف مقابل جهد البوابة إلى المصدر أو ID مقابل VGS.

بمساعدة خصائص التصريف الموضحة على الجانب الأيمن من المحور 'y' ، يمكننا رسم خط أفقي يبدأ من منطقة التشبع للمنحنى الموضح كـ VGS = 0 V حتى المحور الموضح كمعرف.

المستويات الحالية التي تم تحقيقها في الرسمين البيانيين هي IDSS.

ستكون نقطة التقاطع على منحنى المعرف مقابل VGS كما هو موضح أدناه ، لأن المحور الرأسي محدد على أنه VGS = 0 V

لاحظ أن خصائص التصريف تُظهر العلاقة بين حجم خرج التصريف مع حجم إخراج استنزاف آخر ، حيث يتم تفسير المحورين بواسطة متغيرات في نفس المنطقة من خصائص MOSFET.

وبالتالي ، يمكن تعريف خصائص النقل على أنها مخطط لتيار تصريف MOSFET مقابل كمية أو إشارة تعمل كعنصر تحكم في الإدخال.

ينتج عن هذا بالتالي 'نقل' مباشر عبر متغيرات الإدخال / الإخراج ، عند استخدام المنحنى على يسار الشكل 5.15. إذا كانت علاقة خطية ، لكانت قطعة ID مقابل VGS خطًا مستقيمًا عبر IDSS و VP.

ومع ذلك ، ينتج عن هذا منحنى مكافئ بسبب التباعد الرأسي بين VGS الذي يتخطى خصائص التصريف ، والذي يتناقص إلى حد ملموس حيث يصبح VGS سالبًا بشكل متزايد ، في الشكل 5.15.

إذا قارنا المسافة بين VGS = 0 V و VGS = -1V مع المسافة بين VS = -3 V والقرص ، فإننا نرى أن الاختلاف متطابق ، على الرغم من اختلافه كثيرًا في قيمة المعرف.

نحن قادرون على تحديد نقطة أخرى على منحنى النقل عن طريق رسم خط أفقي من منحنى VGS = -1 V حتى محور المعرف ثم تمديده لاحقًا إلى المحور الآخر.

لاحظ أن VGS = - 1V عند المحور السفلي لمنحنى النقل عندما يكون المعرف = 4.5 مللي أمبير.

لاحظ أيضًا أنه في تعريف المعرف عند VGS = 0 فولت و -1 فولت ، يتم استخدام مستويات تشبع المعرف ، بينما يتم إهمال المنطقة الأومية.

بالمضي قدمًا ، مع VGS = -2 V و - 3V ، يمكننا إنهاء مخطط منحنى النقل.

كيفية تطبيق معادلة شوكلي

يمكنك أيضًا تحقيق منحنى نقل الشكل 5.15 مباشرةً من خلال تطبيق معادلة شوكلي (المعادل 5.3) ، بشرط تقديم قيم IDSS و Vp.

تحدد مستويات IDSS و VP حدود المنحنى للمحورين ، ولا تتطلب سوى رسم بضع نقاط وسيطة.

صدق معادلة شوكلي يمكن التعبير عن المعادلة 3.5 كمصدر لمنحنى النقل بالشكل 5.15 بشكل مثالي من خلال فحص مستويات مميزة معينة لمتغير معين ثم تحديد المستوى المقابل للمتغير الآخر ، بالطريقة التالية:

يتطابق هذا مع المؤامرة الموضحة في الشكل 5.15.

لاحظ مدى دقة إدارة العلامات السلبية لـ VGS و VP في الحسابات أعلاه. قد يؤدي عدم وجود علامة سلبية واحدة إلى نتيجة خاطئة تمامًا.

من الواضح جدًا من المناقشة أعلاه ، أنه إذا كانت لدينا قيم IDSS و VP (والتي يمكن الرجوع إليها من ورقة البيانات) ، فيمكننا تحديد قيمة المعرف لأي حجم من VGS بسرعة.

من ناحية أخرى ، من خلال الجبر القياسي يمكننا اشتقاق معادلة (عبر المعادلة 5.3) ، لمستوى VGS الناتج لمستوى معين من المعرف.

يمكن اشتقاق هذا بكل بساطة للحصول على:

الآن ، دعنا نتحقق من المعادلة أعلاه من خلال تحديد مستوى VGS الذي ينتج تيار استنزاف قدره 4.5 مللي أمبير لـ MOSFET لها خصائص تطابق الشكل 5.15.

تتحقق النتيجة من المعادلة لأنها تتوافق مع الشكل 5.15.

استخدام طريقة الاختزال

نظرًا لأننا نحتاج إلى رسم منحنى النقل كثيرًا ، فقد يجد المرء أنه من الملائم الحصول على تقنية مختصرة لرسم المنحنى. تتمثل الطريقة المرغوبة في السماح للمستخدم برسم المنحنى بسرعة وكفاءة ، دون المساومة على الدقة.

تم تصميم المعادلة 5.3 التي تعلمناها أعلاه بحيث تنتج مستويات VGS المعينة مستويات معرف يمكن تذكرها لاستخدامها كنقاط مؤامرة أثناء رسم منحنى النقل. إذا حددنا VGS على أنه 1/2 من قيمة VP للقرص ، فيمكن تحديد مستوى المعرف الناتج باستخدام معادلة Shockley بالطريقة التالية:

يجب ملاحظة أن المعادلة أعلاه لم يتم إنشاؤها لمستوى معين من نائب الرئيس. المعادلة هي شكل عام لجميع مستويات VP طالما أن VGS = VP / 2. تشير نتيجة المعادلة إلى أن تيار التصريف سيكون دائمًا 1/4 من مستوى التشبع IDSS طالما أن الجهد من البوابة إلى المصدر له قيمة أقل بنسبة 50 ٪ من قيمة الضغط.

يرجى ملاحظة أن مستوى معرف VGS = VP / 2 = -4V / 2 = -2V وفقًا للشكل 5.15

اختيار ID = IDSS / 2 واستبداله في المعادلة 5.6 نحصل على النتائج التالية:

على الرغم من أنه يمكن إنشاء المزيد من نقاط العدد ، يمكن تحقيق مستوى كافٍ من الدقة ببساطة عن طريق رسم منحنى النقل باستخدام 4 نقاط مؤامرة فقط ، كما هو محدد أعلاه وأيضًا في الجدول 5.1 أدناه.

في معظم الحالات ، يمكننا استخدام نقطة الرسم فقط باستخدام VGS = VP / 2 ، في حين أن تقاطعات المحور في IDSS و VP ستمنحنا منحنى موثوقًا بدرجة كافية لمعظم التحليل.