انحياز مقسم الجهد في دوائر BJT - مزيد من الاستقرار بدون عامل بيتا

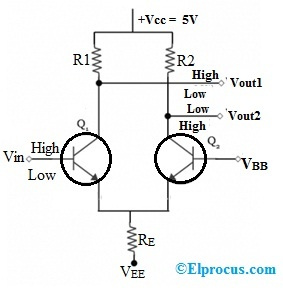
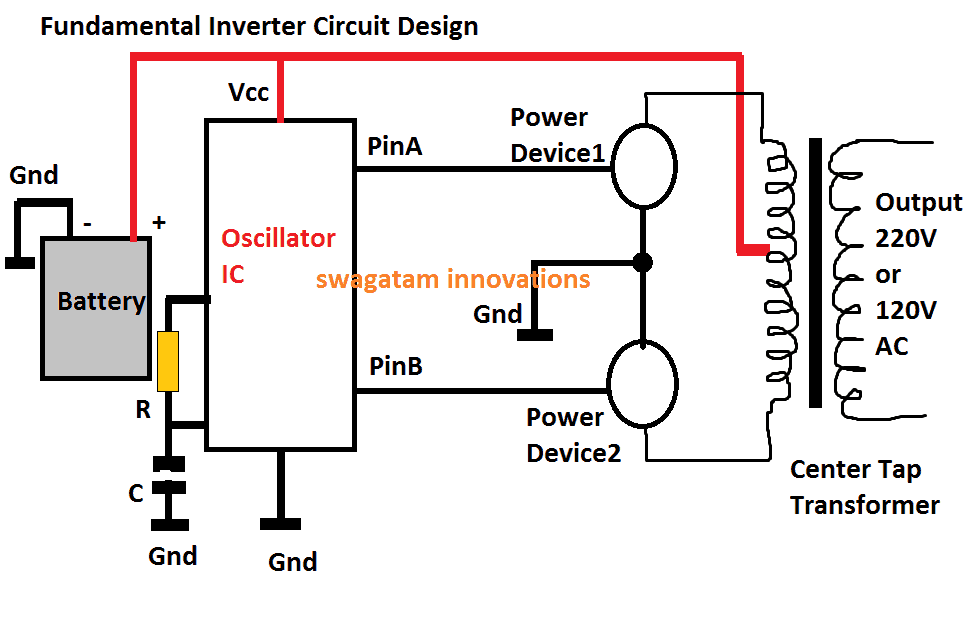
يُطلق على تحيز أطراف الترانزستور ثنائي القطب باستخدام شبكة مقسم مقاومة محسوبة لضمان الأداء الأمثل واستجابة التبديل ، انحياز مقسم الجهد.

في ال تصاميم التحيز السابقة أننا تعلمنا التحيز الحالي أنا CQ والجهد الخامس CEQ كانت دالة للكسب الحالي (β) لـ BJT.

ولكن ، كما نعلم أن β يمكن أن تكون عرضة للتغيرات في درجة الحرارة ، خاصة بالنسبة لترانزستورات السيليكون ، وكذلك القيمة الحقيقية للبيتا غالبًا ما لا يتم تحديدها بشكل صحيح ، فقد يكون من المستحسن تطوير انحياز مقسم الجهد في دائرة BJT التي قد تكون أقل عرضة لدرجات الحرارة ، أو ببساطة مستقلة عن BJT beta نفسها.

يمكن اعتبار ترتيب انحياز مقسم الجهد في الشكل 4.25 أحد هذه التصميمات.

عندما يتم فحصه باستخدام ملف الأساس الدقيق تبدو القابلية للتغيرات في الإصدار التجريبي متواضعة حقًا. إذا تم وضع متغيرات الدائرة بشكل مناسب ، فإن مستويات I CQ و V. CEQ يمكن أن تكون مستقلة تمامًا عن الإصدار التجريبي تقريبًا.

تذكر من التفسيرات السابقة أن النقطة Q تتميز بمستوى ثابت من ICQ و VCEQ كما هو موضح في الشكل 4.26.

درجة أنا BQ يمكن أن يتغير اعتمادًا على الاختلافات في الإصدار التجريبي ، ولكن نقطة التشغيل حول الخصائص التي حددتها أنا CQ و V. CEQ يمكن أن تظل دون تغيير بسهولة إذا تم تطبيق إرشادات الدائرة المناسبة.

كما هو مذكور أعلاه ، ستجد طريقتين يمكن استخدامها للتحقق من إعداد مقسم الجهد.

سيتضح السبب وراء اختيار أسماء معينة لهذه الدائرة خلال تحليلنا ، وستتم مناقشته في المنشورات المستقبلية.

أول واحد هو تقنية دقيقة والتي يمكن إجراؤها على أي إعداد لمقسم الجهد.

الثاني يسمى طريقة تقريبية ويصبح تنفيذه ممكنًا عند استيفاء عوامل معينة. ال نهج تقريبي يتيح تحليلًا مباشرًا بدرجة أكبر بكثير بأقل جهد ووقت.

بالإضافة إلى ذلك ، يمكن أن يكون هذا مفيدًا جدًا لـ 'وضع التصميم' الذي سنتحدث عنه في الأقسام اللاحقة.
على العموم ، منذ 'نهج تقريبي' يمكن العمل مع معظم الشروط وبالتالي يجب تقييمها بنفس مستوى الاهتمام مثل 'الطريقة الدقيقة'.

التحليل الدقيق

دعونا نتعلم كيف طريقة تحليل دقيق يمكن تنفيذها مع الشرح التالي

بالإشارة إلى الشكل التالي ، يمكن إعادة إنتاج جانب الإدخال من الشبكة كما هو موضح في الشكل 4.27 لتحليل التيار المستمر.

ال ما يعادل Thévenin شبكة للتصميم على الجانب الأيسر من قاعدة BJT يمكن تحديدها بطريقة كما هو موضح أدناه:

RTh : يتم استبدال نقاط إمداد الدخل بدائرة قصر مكافئة كما هو موضح في الشكل 4.28 أدناه.

ETh: مصدر جهد التغذية V العاصمة يتم تطبيقه مرة أخرى على الدائرة ، ويتم تقييم جهد Thévenin ذو الدائرة المفتوحة كما يظهر في الشكل 4.29 أدناه كما هو موضح أدناه:

بتطبيق قاعدة مقسم الجهد نصل إلى المعادلة التالية:

بعد ذلك ، من خلال إعادة إنشاء تصميم Thévenin كما هو موضح في الشكل 4.30 ، نقوم بتقييم I BQ من خلال تطبيق قانون جهد كيرشوف أولاً في اتجاه عقارب الساعة للحلقة:

ETh - IBRTh - VBE - IERE = 0

كما نعلم IE = (+ 1) ب استبدالها في الحلقة أعلاه وحل أنا ب يعطي:

معادلة. 4.30

للوهلة الأولى قد تشعر بالمكافئ. يبدو (4.30) مختلفًا تمامًا عن المعادلات الأخرى التي تم تطويرها حتى الآن ، ولكن نظرة فاحصة ستظهر أن البسط هو مجرد فرق بين مستويين من الفولت ، في حين أن المقام هو نتيجة مقاومة القاعدة + باعث المقاوم ، وهو ما ينعكس بواسطة (β + 1) وهو بلا شك مشابه جدًا لـ Eq. (4.17) ( حلقة باعث القاعدة )

بمجرد حساب IB من خلال المعادلة أعلاه ، يمكن تحديد المقادير المتبقية في التصميم بنفس الطريقة كما فعلنا مع شبكة التحيز الباعث ، كما هو موضح أدناه:

المعادلة (4.31)

حل مثال عملي (4.7)
احسب جهد تحيز التيار المستمر V هذه وأنا الحالي ج في شبكة مقسم الجهد الموضحة أدناه الشكل 4.31

الشكل 4.31 دائرة مثبتة بيتا للمثال 4.7.

تحليل تقريبي

في القسم أعلاه تعلمنا 'الطريقة الدقيقة' ، سنناقش هنا 'الطريقة التقريبية' لتحليل مقسم الجهد لدائرة BJT.

يمكننا رسم مرحلة الإدخال لشبكة مقسم الجهد القائمة على BJT كما هو موضح في الشكل 4.32 أدناه.

يمكن اعتبار المقاومة Ri بمثابة مقاومة مكافئة بين خط القاعدة والأرض للدائرة ، و RE كمقاومة بين الباعث والأرض.

من مناقشاتنا السابقة [Eq. (4.18)] نعلم أن المقاومة المعاد إنتاجها أو المنعكسة بين القاعدة / باعث BJT يتم شرحها بواسطة المعادلة Ri = (+ 1) RE.

إذا أخذنا في الاعتبار موقفًا يكون فيه Ri أكبر بكثير من المقاومة R2 ، فسوف ينتج عنه IB أصغر نسبيًا من I2 (تذكر أن التيار يحاول دائمًا إيجاد الاتجاه الأدنى للمقاومة والانتقال إليه) ، وبالتالي فإن I2 سوف يتحول تقريبًا إلى مساوٍ لـ I1.

بالنظر إلى أن القيمة التقريبية لـ IB هي في الأساس صفر بالنسبة إلى I1 أو I2 ، فيمكن اعتبار I1 = I2 و R1 و R2 كعناصر متسلسلة.

الشكل 4.32 دائرة التحيز الجزئي لحساب جهد القاعدة التقريبي V. ب .

يمكن تقييم الجهد عبر R2 ، والذي سيكون في الأصل الجهد الأساسي كما هو موضح أدناه ، من خلال تطبيق شبكة قاعدة مقسم الجهد:

الآن منذ ذلك الحين Ri = (β + 1) RE ≅ ب إعادة، الشرط الذي يؤكد ما إذا كان تنفيذ الطريقة التقريبية ممكنًا أم لا يتم تحديده بواسطة المعادلة:

ببساطة ، إذا كانت قيمة RE تضاعف قيمة ، لا تقل عن 10 أضعاف قيمة R2 ، فقد يُسمح بتنفيذ التحليل التقريبي بدقة مثالية

بعد تقييم VB ، يمكن تحديد حجم VE بالمعادلة:

بينما يمكن حساب تيار المرسل بتطبيق الصيغة:

يمكن تحديد الجهد من المجمع إلى الباعث باستخدام الصيغة التالية:

VCE = VCC - اللجنة الدولية للصليب الأحمر - IERE

لكن منذ IE ≅ IC ، نصل إلى المعادلة التالية:

تجدر الإشارة إلى أنه في سلسلة العمليات الحسابية التي أجريناها من المعادلة. (4.33) من خلال Eq. (4.37) ، فإن العنصر β ليس له وجود في أي مكان ، ولم يتم حساب IB.

هذا يعني أن نقطة Q (كما حددتها I CQ و V. CEQ ) نتيجة لذلك لا تعتمد على قيمة β
مثال عملي (4.8):

دعونا نطبق التحليل في وقت سابق الشكل 4.31 ، باستخدام نهج تقريبي ، ومقارنة الحلول لـ ICQ و VCEQ.

نلاحظ هنا أن مستوى VB مطابق لمستوى ETh ، كما تم تقييمه في مثالنا السابق 4.7. ما يعنيه هذا في الأساس هو أن الفرق بين التحليل التقريبي والتحليل الدقيق يتأثر بـ RTh ، وهو المسؤول عن فصل ETh و VB في التحليل الدقيق.

المضي قدما،

المثال التالي 4.9

دعنا نجري التحليل الدقيق للمثال 4.7 إذا تم تقليل β إلى 70 ، واكتشف الفرق بين حلول ICQ و VCEQ.

المحلول
قد لا يتم أخذ هذا المثال كمقارنة بين الاستراتيجيات الدقيقة مقابل الإستراتيجيات التقريبية بدلاً من ذلك فقط لاختبار الدرجة التي يمكن أن تتحرك فيها نقطة Q في حالة انخفاض حجم β بنسبة 50٪. يتم إعطاء RTh و ETh على النحو نفسه:

يعطينا ترتيب النتائج في شكل جدول ما يلي:

من الجدول أعلاه يمكننا أن نكتشف بوضوح أن الدائرة غير مستجيبة نسبيًا للتغيير في β المستويات. على الرغم من حقيقة أن β الحجم قد انخفض بشكل كبير بنسبة 50٪ ، من قيمة 140 إلى 70 ، على الرغم من أن قيم ICQ و VCEQ هي نفسها بشكل أساسي.

المثال التالي 4.10

تقييم مستويات أنا CQ و V. CEQ لشبكة مقسم الجهد كما هو موضح في الشكل 4.33 من خلال تطبيق بالضبط و تقريبي النهج ومقارنة الحلول الناتجة.

في السيناريو الحالي ، الشروط الواردة في المعادلة. (4.33) قد لا تكون راضية ، ولكن الإجابات قد تساعدنا في تحديد الاختلاف في الحل مع شروط المعادلة. (4.33) لم تؤخذ بعين الاعتبار.
الشكل 4.33 مقسم الجهد شبكة على سبيل المثال 4.10.

الحل باستخدام التحليل الدقيق:

الحل باستخدام التحليل التقريبي:


من التقييمات المذكورة أعلاه يمكننا أن نرى الفرق بين النتائج المحققة من الطرق الدقيقة والتقريبية.

تظهر النتائج أنني CQ هو حوالي 30٪ أعلى للطريقة التقريبية ، بينما V. CEQ هو 10٪ أقل. على الرغم من أن النتائج ليست متطابقة تمامًا ، بالنظر إلى حقيقة أن βRE أكبر بثلاث مرات من R2 ، فإن النتائج في الواقع ليست متباعدة جدًا أيضًا.

قال أنه لتحليلنا المستقبلي سنقوم في الغالب بالاعتماد على المعادلة. (4.33) لضمان أقصى قدر من التشابه بين التحليلين.